

Why are vertical angles congruent? (Answer: If angle 1 and angle 2 are supplementary and angle 2 and 3 are supplementary, then angle 1 and angle 3 must be congruent.).

Which angles are congruent? Why do you think they are congruent?.What is the sum of the four angle measures in the middle of the paper? Why?.Are all of these pairs of angles adjacent?.On your sheet of paper, which angles are supplementary?.They are all right angles.įacilitate the discussion to help students understand the mathematics of the lesson. If angles 3, 4, 5, and 6 are congruent, they all have a measure of 90°.If angles 1 and 2 are congruent, they both have a measure of 90°.In the third sketch, students should notice that the angle sum is always 90° and that the angles are complementary. In the second sketch, students should notice the sum of the supplementary angles and the congruent vertical angles. As one angle increases in size, the other decreases. In the first sketch the angles are always supplementary.If the sides of the angle were longer or shorter, would the measure of the angle change?.Student thinks that the length of the ray affects the size of the angle. At the measure of each angle shown on the protractor, what do you notice about the sum of the two angles shown?.Student does not see that the adjacent angles are supplementary. Most students will be able to generalize about supplementary angles and vertical angles, particularly after using the sketches and seeing repeated cases.Mathematical Practice 8: Look for and express regularity in repeated reasoning. This leads to several pairs of supplementary angles that are not adjacent: angles 5 and 10, angles 6 and 9, angles 7 and 12, and angles 8 and 11 (again, a preview of angles formed by a transversal).įor the Angles Sketch interactive, have students work individually or with a partner. They should also see that angles 5 and 9, angles 6 and 10, angles 7 and 11, and angles 8 and 12 are congruent (a preview of angles formed by a transversal). Angles 5 and 6, angles 7 and 8, angles 9 and 10, and angles 11 and 12 are all supplementary.(These are vertical angles.) Students may also notice that the four angle measures add up to 360°. They should also see that angles 1 and 3, and angles 2 and 4 are congruent. Angles 1 and 2, angles 2 and 3, angles 3 and 4, and angles 4 and 1 are all supplementary.It is labeled to make it easier to refer to specific angles. The rectangle shown is an example of what the folded sheet of paper might look like.Is the angle opening to the left or right?.Is the angle measure greater than or less than 90°?.Student does not read the protractor and/or interpret the angle correctly.

Is the vertex at the center of the protractor?.
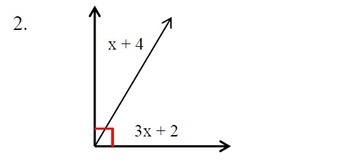


 0 kommentar(er)
0 kommentar(er)
